Ridge Regression Classifier
Ridge regression is a regularization technique and an extension of linear regression where the loss function is altered by adding a penalty equivalent to the square of the magnitude of the coefficients.
Detailed Understanding
In a standard linear equation, we try to minimize the error between our predictions and actual values. In ridge regression, we try to minimize this same error, but with a penalty term added. This penalty term is the L2 regularization which is the square sum of magnitude of coefficient values multiplied by lambda.
The ridge coefficients minimize a penalized residual sum of squares:
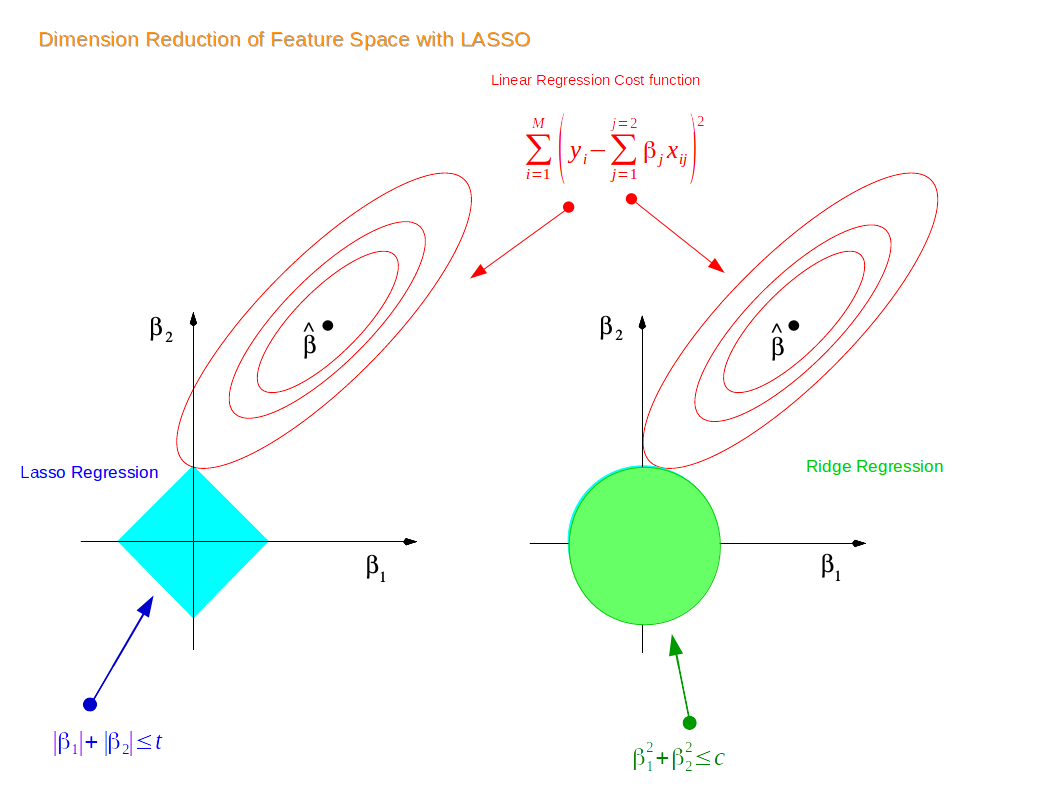
where, α >= 0 is a complexity parameter that controls the amount of shrinkage: the larger the value of α, the greater the amount of shrinkage and thus the coefficients become more robust to collinearity.
Implementation in Python
from sklearn.model_selection import train_test_split
from sklearn.linear_model import Ridge
# create feature matrix (X) and target vector (y)
X = data[data.columns.tolist()[:-1]]
y = data[data.columns.tolist()[-1]]
# split the dataset into training set and test set
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)
# Create Ridge regression object
ridge = Ridge(alpha=1.0)
# Train the model using the training sets
ridge.fit(X_train,y_train)
Advantages and Disadvantages
Advantages
- Ridge regression allows you to regularize or shrink coefficient estimates towards zero, to prevent overfitting.
- Ridge can handle multicollinearity and high-dimension data well by introducing bias.
- It includes all the features in the model.
Disadvantages
- It includes all the features in the model, so can lead to overfitting, even though it reduces the coefficient magnitude.
- It introduces bias in its predictions.
- The regularization parameter (α) selection is tricky.
When can we use Ridge Regression?
Ridge regression can be used when we need to analyze multiple regression data that suffer from multicollinearity. When multicollinearity occurs, least squares estimates are ‘unstable’, so slight changes to the input data can lead to large changes in the model estimate. Ridge regression stabilizes these estimates and provides a way to create more reliable, interpretable models.