ElasticNet Regression

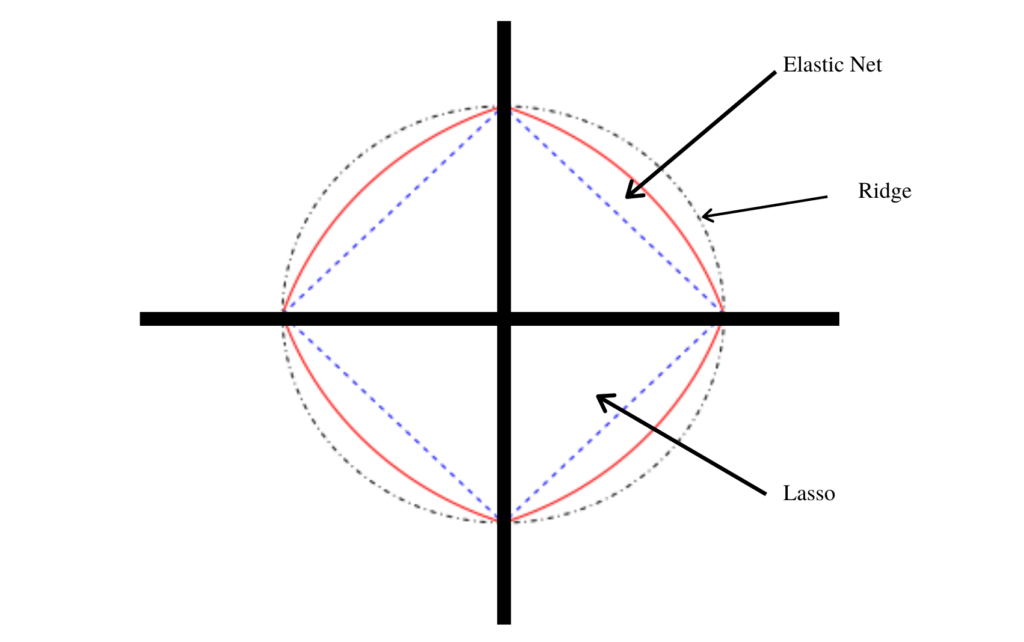
ElasticNet is a linear regression model trained with both L1 and L2-norm regularization of the coefficients. This combination allows for learning a sparse model where few of the weights are non-zero like Lasso, while still maintaining the regularization properties of Ridge.

Elastic-net is useful when there are multiple correlated features.

How it works

Roughly speaking, ElasticNet is a model which combines both L1 and L2 regularization of Lasso and Ridge methods:

Lasso helps to reduce overfitting by setting some feature coefficients to zero thus completely eliminating them and Ridge Regression helps to control the multicollinearity effect.

ElasticNet incorporates penalties from both L1 and L2 regularization:

Where,

• λ is the tuning parameter
• α is the proportion of L1 penalty and 1- α is the L2 penalty.

Python Example

Here is a simple implementation of ElasticNet Regression in Python using the sklearn library.

    from sklearn.linear_model import ElasticNet
    from sklearn.datasets import make_regression

    # Generate a regression data set
    X, y = make_regression(n_features=2, random_state=0)

    # Define the model
    regr = ElasticNet(random_state=0)

    # Train the model
    regr.fit(X, y)

    # Print the coefficients
    print(regr.coef_)

The above code creates a simple regression model, fits it to the data X, y, and then prints out the coefficients of the model.

Advantages

1. It combines the L1 & L2 properties, It works well on some specific datasets where the features are correlated.
2. It has built-in feature selection.
3. It's efficient when dealing with large number of features.

Disadvantages

1. It includes a hyper-parameter that needs to be tuned, so computational expense is an issue.
2. Performance is compromised when we have uncorrelated variables.

When to use ElasticNet Regression?

ElasticNet is a middle ground between Ridge Regression and Lasso Regression. The α parameter is a mix ratio between Ridge and Lasso, giving some balance between the two.

• When you have highly correlated variables, Ridge regression makes sense.
• When you have sparse data or wish to automate certain parts of model selection, the Lasso makes sense.
• If multicollinearity is suspected in your dataset and/or you wish to automate certain parts of model selection, an Elastic Net could work.

Conclusion

ElasticNet is a powerful tool that combines the benefits of two other regression methods. It is, however, more complex and requires careful tuning of its parameters. In return, it can bring substantial benefits in terms of model accuracy, especially for datasets exhibiting multicollinearity.