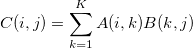Linear Algebra
Linear Equations
Structure
One of the most basic motivations towards making computers was solving a system linear equations given by
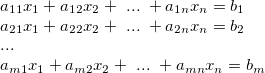
where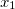 
, 
, ... 
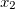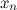are unknowns and 
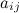's and 
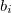's denote the constants, either complex or real.
Definitions
A system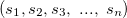 
is called a solution of the above system of linear equations if 
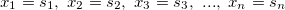satisfies each of the eqations in our system of linear equations simultaneously and when 
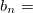
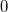, then the system of equations is called to be homogeneous. Such system of equations have one certain solution 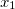= 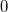, 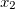= 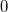, ... 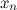= 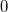called the trivial solution. A system of Linear equations is said to be consistent if it has at least one solution and inconsistent if it has no solutions.
Vectors
A vector is a numeric measurement with directions. In two dimensions, a vector 
is of the form 
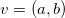and the magnitude of this vector is given by
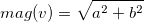
Vector Multiplications
Dot Product
There are two ways to go about this:
-
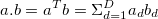
This is the summation of element wise multiplication of the two vectors. The notation
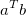denotes that the vectors are column vectors and the result of the equation above would be a 1x1 vector which is a scalar quantity. -
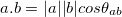
This notation is not very convenient for vector multiplication unless a the angle on the right hand side is known to us. Although, it is a much more common practice to use this equation for finding out the angle between two vectors using
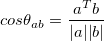
Outer Product
The outer product of two vectors results in a matrix and is given by the equation:
If there are two column vectors u1 and v1 that are given by 
and 
respectively. Then their outer product is written as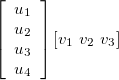 
which then results to be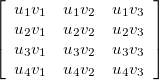 
.
Matrices
Matrices are two dimensional set of numbers. These are very efficient data types for quick computations.
Matrix Multiplications
Dot Product
The product of two matrices A and B in given by the formulae
