Stochastic Gradient Descent Classifier
Stochastic Gradient Descent (SGD) is a simple yet efficient approach to fit linear models. It's an efficient way of implementing linear classifiers and regressors under convex loss functions, such as huber, epsilon_insensitive, squared_loss, and more.
Explanation
In an iterative manner, SGD selects one training sample at each step and computes the gradient of the loss function. In simpler terms, SGD tries to find minimums or maximums by iteration.
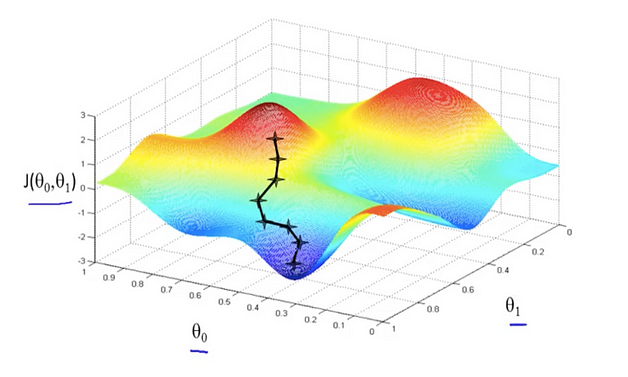
Below is a representation of how SGD function estimates parameters in a gradient descent manner:
Python Explanation
from sklearn.linear_model import SGDClassifier
# Initializing the model
clf = SGDClassifier(loss="hinge", penalty="l2", max_iter=5)
# Training the model
clf.fit(X, Y)
# Predicting the output
clf.predict([[-0.8, -1]])
In the above example, we first import SGDClassifier from sklearn.linear_model. We initialize the classifier with the hinge loss and l2 penalty. We train the model using clf.fit() function and predict the output using clf.predict() function.
Advantages
- Efficiency: SGD allows training on large scale data due its efficiency. It is well-suited for 'online' learning setting.
- Ease of implementation: It provides a lot of opportunities for code tuning.
Disadvantages
- No Guaranteed Convergence: One disadvantage of SGD is that it does not always guarantee to rapidly converge.
- Hyperparameters: Requiring a number of hyperparameters such as the regularisation parameter and the number of iterations.
- Sensitive to feature scaling: It is sensitive to feature scaling, that is it does not work well when the features are not on a relatively similar scale.
Usage Scenario
SGD is used in a variety of applications. It is excellent for large-scale and sparse machine learning problems, often encountered in text classification and natural language processing.
If the data is sparse, the code in SGDClassifier easily scales to problems with more than 10^5 training examples and more than 10^5 features.