K-Nearest Neighbors Classifier

K-Nearest Neighbors (K-NN) is one of the simplest machine learning algorithms. It is a type of instance-based learning where the function is only approximated locally and all computation is deferred until classification. The K-NN algorithm is a non-parametric method used for both regression and classification problems.

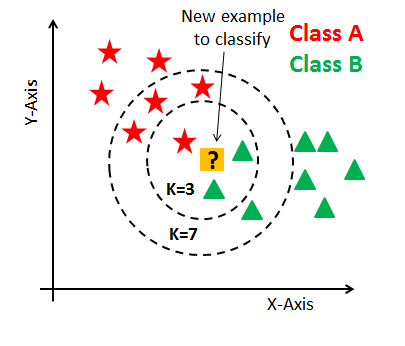
When the K-NN is used for classification, the output is a class membership. An object is assigned to the class most common among its K nearest neighbors, where K is a positive integer, typically small. If K = 1, then the object is simply assigned to the class of that single nearest neighbor.

How does it work?

K-NN works on the principle of similarity or proximity. Here are the general steps:

1. A positive integer K is specified.
2. The K nearest data points are selected based on a distance metric.
3. The majority class among the K nearest neighbors is then assigned to the test point.

If a data point is in close vicinity to several points that belong one category, chances are it'll belong to that same category.

Python Implementation

The Scikit-learn library in Python provides a function called KNeighborsClassifier from the sklearn.neighbors package, that can be used to implement K-NN.

from sklearn.neighbors import KNeighborsClassifier
knn = KNeighborsClassifier(n_neighbors=3)
knn.fit(X_train, y_train)

• n_neighbors is the parameter to set the K value. It's the number of neighbors to consider.
• fit() function fits the model to the training data.
• We can then use predict() function to predict the class labels.

knn.predict(X_test)

Where X_test is the testing data which the classifier will predict.

Choosing the correct K value

Choosing the value of K can be tricky. A low value for K will be influenced by the noise in the data and a high value will be more computationally expensive. As a general guideline a good starting point for K is sqrt(n) where n is total number of data points.

A commonly used method is to choose K is the cross-validation.

Using the cross-validation, we could calculate the accuracy of the K-NN algorithm for different K values. Then the K with the highest accuracy could be chosen.

Advantages

• No assumptions about data — useful, for example, for nonlinear data
• Simple algorithm — to explain and understand/interpret
• High accuracy (relatively) — it is pretty high but not competitive in comparison to better supervised learning models

Limitations

• Computationally expensive — because the algorithm stores all of the training data
• High memory requirement — Stores all (or almost all) of the training data
• Prediction stage might be slow with big N
• Sensitive to irrelevant features and the scale of the data

In summary, the K-NN algorithm is good for large dataset with fewer attributes (low dimensional space) and where data points are more uniformly spread.

K-Nearest Neighbors (KNN) Classifier

The K-nearest neighbors (KNN) algorithm is a type of instance-based learning, or lazy learning. This classifier algorithm measures the distance between samples and classify them based on it.

Advantages:

1. No Assumption About Data: The algorithm makes no assumption about the underlying data distribution pattern which makes it very useful for nonlinear data.

2. Updating Algorithm: New training examples can be added easily to model, thereby this approach remains robust in changing scenarios.

3. Ease Of Use: It’s a very simple and easy to understand Machine Learning algorithms yet powerful tool,

4. Naturally handles multi-class cases: Different classes in target variable are treated equally irrespective to their frequency.

5. Robust to noisy training data : Works well with noise in the dataset as long as noise does not completely obscure the signal.

Disadvantages:

1. Computationally Expensive: As the dataset grows efficiency or speed of algorithm declines rapidly due to its operation in calculating distances from each point to every other point in the dataset

2. Normalization Of Dataset: Before applying KNN, normalization should always be performed; otherwise higher ranged features might dominate when computing distance.

3. Sensitive To Noisy And Missing Data: Outlier values will mislead prompting faulty analysis

4. Doesn’t work well with high dimensional data: As dimensions increase model begins losing significant performance due “Curse Of Dimensionality”.

5. Dimensions sensitivity : As dimensions/features increases its effectiveness decreases due increased space leading curse dimensionality.

Appropriate Usage Scenarios:

1.K- Nearest-Neighbors widely used for both Classification & Regression predictive problems .

2: If your problem requirement doesn’t involve time constraint you plan on working with small datasets

In those cases where numerical output variable based prediction is not required.

3: Classification problems where you have labelled data such as spam detection,email classification etc

4: Recommender Systems - once trained ,the k- nearest neighbours of product can suggest similar items

5: Features have identical scales – since k-NN work by calculating distances if range are not comparable then normalisation needed else use different approach

May incur problem dealing these scenarios :

• Large Datasets: Given computational cost typically doesn't turn out huge datasets,

• High Dimensions: Due Curse dimensionality avoid it using high-dimension spaces.