Numpy

Numpy is a library used specifically for advanced and faster data manipulation in Python. It allows us to effectively manage and manipulate our datasets with minimal programming. In this document, we will have a look at what are the most commonly used features of Numpy and how can we exploit them to optimize our Python programming.

Import Data

1. Read a csv: A csv file containing only numerical data can be imported using np.loadtext('filepath.csv', delimiter = ","). The default delimiter is whitespace so explicit definition is required.
2. No Headers: If the first row contains header, the skiprows = 1 argument must be used to skip the first row.
3. Selective column import: If only a certain number of columns are required to be imported, then we can use usecols = [0,1,4] attribute with column indices to import only a few of all columns possible.
4. Import columns with different datatypes: Although not recommended, Numpy has the ability to import dataframe like structures which contain different datatypes in different columns. This can be done using np.genfromtxt() function. Refer documentation for more.

Arrays

2-D Arrays

We can create 2-D Numpy arrays as a = np.array([[1,2,3], [4,5,6]]) and this would lead to a 2 dimensional array with 2 rows and 3 columns.

On this object, the attribute shape represents the dimensions. It can be used as a.shape to return (2,3) meaning 2 rows and 3 columns exist in this 2D array.

Iteration

If iteration is required over every single element in a 2-D Array using a for loop, then the method np.nditer must be used in the following syntax:

for val in np.nditer(my_np_array):
    do_something(val)

The iteration in the case above will happen in a row wise fashion. First observation will be iterated over (and all features of this row will be called), and then the second row and so forth.

Mathematics on Vectors

Random Operations

1. In order to generate a simple random number, np.random.rand() can be used. This would result in a random number between 0 and 1.
2. We can set a seed using the function np.random.seed(seedValue) which would then introduce reproducability between our function calls.
3. Random integers from a select range of integers can be generated using np .random.randint(start_integer, end_integer) which in this case would result in random integers between start_integer and end_integer - 1 (because the end of range is not included in Python).

Dot Products

The dot products can be defined for two vectors or matrices in the following ways:

1. 

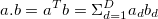
   This is the summation of element wise multiplication of the two vectors. The notation 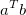denotes that the vectors are column vectors and the result of the equation above would be a 1x1 vector which is a scalar quantity.

   This definition can be emulated in Python (using Numpy) in various ways:

   1. Without using Numpy functions)

      # Create the necessary variables
      dotProd = 0
      a = np.array([1,2,3])
      b = np.array([2,3,4])
      
      # Use a for-loop to calculate the dot product
      for e,f in zip(a,b):
          dotProd += e*f
      
      
      # The value of dot now becomes 20 as one would expect
      

   2. Using np.sum function

      dotProd = np.sum(a*b)
      
      # The value of dotProd will be the same as the generic 
      # code we wrote above because the a*b notation creates 
      # a vector of products of individual elements and then
      # we just sum them to emulate the equation above
      

   3. Using the sum function over the np.array object instances

      dotProd = (a*b).sum()
      
      # Notice the use of object's sum function instead of
      # using the sum function of the class as in Method 2
      

   4. Using the np.dot function

      dotProd = np.dot(a,b)
      

   5. Using the dot function over the np.array object instances

      dotProd = a.dot(b)
      
      # Notice the use of object's dot function instead of
      # using the dot function of the class as in Method 4
      

   for loops should be avoided whenever possible. The intrinsic functions of Numpy are magnitudes faster in operation.

2. 

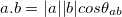
   This notation is not very convenient for vector multiplication unless a the angle on the right hand side is known to us. Although, it is a much more common practice to use this equation for finding out the angle between two vectors using

   

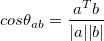
   Let's use this equation to find the angle between the vectors above step by step:

   1. Find the magnitudes of the vectors.

      # We can do this in two ways:
      
      # Option 1: Without using the built-in Numpy function 
      # for this task
      magA = np.sqrt(a.dot(a))
      
      # Option 2: Using the Linear Algebra module of the 
      # Numpy package to do this task
      magA = np.linalg.norm(a)
      
      # Using the equation in the starting of this chapter
      

   2. Calculate the cosine of the angle between the two vectors. We know from the equation shown above that the angle between the two vectors can easily be calculated if we have the magnitudes of the two vectors and their cross product.

      costheta = a.dot(b) / ( np.linalg.norm(a) * np.linalg.norm(b) )
      

   3. Once we have done this, the actual angle can easily be calculated by using the np.arccos function of the Numpy Library

      theta = np.arccos(costheta)
      

      The value that we obtain for theta from the operation above is in radians.

Outer Products

This function takes in two vectors a and b and then returns their outer product.

AOuter = np.outer(a, b)

Matrix

A matrix is an inherent data type in Numpy but it can also be an array of arrays if we don't want it t be a matrix. The official NP documentation discourages the use of matrices and encourages users to use array of arrays notation instead. This requires all arrays to be of the same length however, obviously. it can be defined as M = np.array([[1, 2], [3, 4]]) which would then define an array of array kind of matrix immediately.

To access a particular element, [i, j] notation may be used, just like data frames.

Create a matrix

We can create an empty matrix by using the np.zeros((5, 5)) which would return a 5 by 5 matrix of zeros. Similarly np.ones can be used to create a matrix of ones.

Mathematics on Matrices

Multiplication of Matrices

The definition of matrix is given in the prerequisites section of this book.

1. A simple operation like matrix multiplication can be easily done by using the .dot() function of Numpy stack. therefore for two matrices A and B, their multiplicative result would be given by C = A.dot(B). This would result in the matrix multiplication of the two matrices A and B.

2. In order to do an element wise multiplication in matrices we can simply say A*B and this would result in each element of one matrix to be multiplied by the corresponding element in the other matrix.

Other common mathematical operations on a Matrix

A = np.array([[1, 2], [3, 4]])
Ainv    = np.linalg.inv(A)  // Gives us the inverse of A
Adet    = np.linalg.det(A)  // Gives us the determinant of A
Adiag   = np.diag(A)            // Gives us the diagonal elements of A in a vector
Atrace = np.trace(A)        // Gives us the sum of diagonal elements of A

If you pass a 2D Array to np.diag, then it returns the diagonal elements, if you a pass a 1D array however, it returns a 2D Array with all off diagonal elements as 0 and the elements of the array as diagonal elements.

Solving a Linear System

The problems in a linear system are often of the form 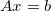. The solution for x, is easily given by 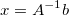. We are assuming that A is a square matrix and is invertible. The system has D equations and D unknowns to solve for. This can be simply done by using the equation above and the basic Numpy methods we have used thus far:

x = np.linalg.inv(A).dot(b)     // Method 1
x = np.linalg.solve(a, b)       // Method 2 (Recommended)

Operator overloading in 'np'

Mathematical Operators

a = [1, 2, 3]
print(a+a) 

would return [1,2,3,1,2,3] but if you perform the operation with numpy as follows:

a = np.array([1,2,3])
print(a+a)

would return the element wise sum of the array, i.e. [2,4,6]

Boolean Operators

In case of Boolean Operators over Numpy arrays, the preferred method of operation is using the Numpy function, logical_and(), logical_or() and logical_not(). These are Numpy array equivalents of and, or and not found in base Python.

FAQs

1. What is the difference between a List and an NP Array?

There are several differences between an NP Array and a Python List:

1. There is no append method on a NP Array while the method works well on Python Lists.
2. Lists can be added with a + operator.
3. If L1 = [1, 2] and L2 = [3, 4], adding two lists would gives us the concatenation of those lists (L3 = L1 + L2 would give us the value of L3 as [1, 2, 3, 4]) but adding two Numpy Array would give us the element wise sum for the two Arrays. For example for a Numpy array A = np.array([1, 2]), doing A + A would give us the value of A to be array([2, 4]).
4. Numpy lists can be multiplied and added to elements, while the same is not possible with Python Lists. Doing 2 * L1 would repeat all elements in L1 but doing 2 * A would multiply each element of the Numpy Array with the constant.
5. Almost all mathematical operations are applied element-wise when you are working with Numpy arrays but won't do so with Lists.
6. It's almost always better to use NP arrays for doing mathematical operations and creating mathematical objects.